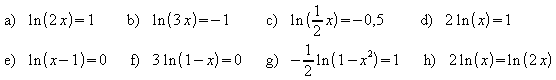5. Der natürliche Logarithmus

Die e-Funktion ist - wie jede Exponentialfunktion - streng monoton wachsend auf, d.h. sie ist umkehrbar. Die Gleichung

wird mit dem Logarithmus von y zur Basis e nach x aufgelöst:

.

Man nennt x den natürlichen Logarithmus von y.
 
Def.: Die Funktionheißt natürliche Logarithmusfunktion.

Ableitung der ln-Funktion

Die Funktionsgleichungwird exponenziert:

,

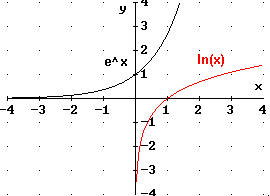
und die so entstandene Gleichung wird abgeleitet:

.

Daraus folgt

,

also:

Daraus erhält man wieder eine Integrationsregel:

.

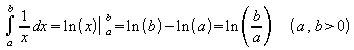Fragen und Übungen

1. Was versteht man unter dem natürlichen Logarithmus einer positiven reellen Zahl?

2. Welche Definitionsmenge und welche Wertemenge besitzt die natürliche Logarithmusfunktion?

3. In welcher Beziehung stehen die e-Funktion und die ln-Funktion?

4. Geben Sie die Ableitung der ln-Funktion an.

5. Bestimmen Sie 3 Stammfunktionen zu.

6. Berechnen Sie das Integral.

7. Wie groß ist der Inhalt der Fläche, den die x-Achse und der Graph der Funktion zwischen x = 1 und x = 2 einschließen?

8. Skizzieren Sie den Graphen von. Beschreiben Sie ihn in Worten und vergleichen Sie ihn mit dem Graphen von.

9. Wo schneidet die Tangente an den Graphen der ln-Funktion bei x = 2 die x-Achse?

Exponentialgleichungen

Gleichungen, in denen die Variable im Exponenten auftreten, heißen Exponentialgleichungen. Zum Lösen solcher Gleichungen wird der Logarithmus verwendet.

Beispiel 1:

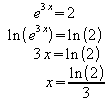
Beispiel 2:

.

Da, kann dies nur erfüllt sein, wennist.

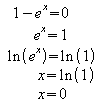
Beispiel 3:

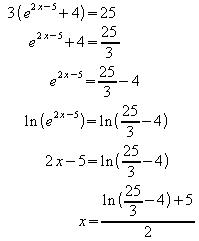
Beispiel 4:

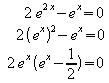
Da, kann dies nur erfüllt sein, wennist also:

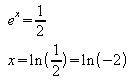
Fragen und Übungen

1. Lösen Sie die folgenden Gleichungen.

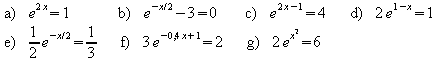
2. Untersuchen Sie, ob die folgenden Gleichungen Lösungen besitzen.

3. Lösen Sie die folgenden Gleichungen durch Exponenzieren.