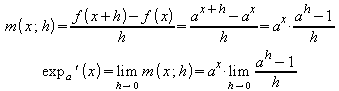4. Die e-Funktion

Um die Ableitung der Exponentialfunktion zur Basis a zu bilden, wird zunächst der Differenzenquotient gebildet:

.

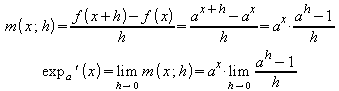Die Ableitung wäre besonders einfach, wenn gilt

.

Gibt es eine Basis a, für die das zutrifft? Der Grenzwert bedeutet ja die Ableitung der Exponentialfunktion zur Basis a an der Stelle x = 0. Es ist also nach einer Exponentialfunktion zu suchen, für die die Tangente an den Graphen bei x = 0 die Steigung 1, also den Steigungswinkel 45° hat.

Die Untersuchung der Graphen von exp2(x) = 2x und exp3(x) =3x zeigt: Für a = 2 ist die Steigung deutlich zu klein, für a =3 ist die Steigung etwas zu groß.
 

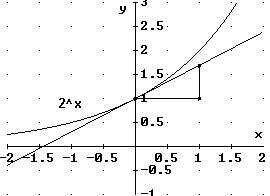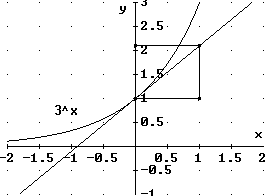Rechnerisch lässt sich feststellen:
 

Die Basis derjenigen Exponentialfunktion, deren Ableitung an der Stelle x = 0 den Wert 1 besitzt, liegt also zwischen 2 und 3, und zwar näher an 3. Diese Zahl wird mit e (Euler'sche Zahl) bezeichnet. Für diese Zahl gilt dann

.

Die Exponentialfunktion zu dieser Basis heißt „natürliche Exponentialfunktion“ oder kurz „e-Funktion“ und wird bezeichnet mit

.

Die Zahl e

Aus dem Grenzwertlässt sich ablesen: Wenn h „klein“ ist, dann gilt

Aus dieser Betrachtung entsteht die Vermutung, dass

ist. Dies trifft zu, wie exakt gezeigt werden kann. Wählt man speziell die Nullfolge h = 1/n, so ergibt sich

 
n
1
10
102
103
104
105
106
2
2,593742
2,704813
2,716923
2,718145
2,718268
2,718281

Der Taschenrechner liefert für e1 die Anzeige 2,718281828. Der Eindruck, dass eine Periode vorliegt, täuscht jedoch. Tatsächlich kann gezeigt werden, dass e eine irrationale Zahl ist.

Eigenschaften der e-Funktion

1. Die Funktionswerte sind immer positiv:

.

2. Grenzwerte:

(Der zweite Grenzwert ist nicht als Zahl zu verstehen. Die Schreibweise bedeutet nur: die Funktionswerte der e-Funktion wachsen über alle Grenzen, wenn x beliebig groß wird.)

3. Die Ableitung der e-Funktion ist mit der Funktion identisch:

.

4. Die e-Funktion ist streng monoton wachsend auf.

5. Die e-Funktion ist eine Stammfunktion zu sich selbst, daher ist:

.

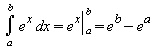Fragen und Übungen

1. Welche besondere Bedeutung hat die Euler'sche Zahl e für die Exponentialfunktionen?

2. Von welcher der folgenden Zahlenmengen ist e ein Element?

3. Geben Sie den Wert von e auf 5 Nachkommastellen genau an.

4. Welche Eigenschaften haben die Funktionswerte der e-Funktion?

5. Wie verhält sichfür?

6. Geben Sie die Ableitung der e-Funktion an.

7. Berechnen Sie die Steigung der Tangente an den Graphen der e-Funktion an den Stellen x = -2 ; -1 ; 0 ; 1 ; 2.

8. Geben Sie drei Stammfunktionen zuan.

9. Wie groß ist der Inhalt der Fläche, den die x-Achse und der Graph der e-Funktion zwischen x = 1 und x = 2 einschließen?

10. Skizzieren Sie den Graphen von. Beschreiben Sie ihn in Worten und vergleichen Sie ihn mit dem Graphen der e-Funktion.

11. Geben Sie die Gleichung der Tangente an den Graphen der e-Funktion an für x = 0 ; 1 ; 2.
Bestimmen Sie jeweils die Stelle x0, an der die Tangente die x-Achse schneidet.