2. Exponentialfunktionen

1. Von einer Potenz  kann man auf zwei Weisen zu einer Funktion kommen.

Bei Potenzfunktionen ist die Basis die Variable: . Die Definitionsmenge ist dabei nach dem Exponenten zu wählen.

Bei Exponentialfunktion ist die Hochzahl die Variable: .
 

Def.: Für  heißt  Exponentialfunktion zur Basis a.

Beispiele:

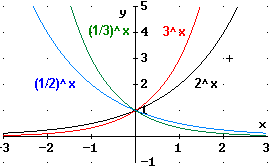
Die Graphen lassen vermuten, dass eine Exponentialfunktion - unabhängig von der Basis a - immer positive Funktionswerte annimmt. Dies trifft tatsächlich zu, wie hier aber nicht bewiesen werden soll:
 

Die Wertemenge einer Exponentialfunktion  ist : .

Aus den Definitionen für Potenzen (s. Abschnitt 1) ergeben sich sofort einige spezielle Werte der Exponentialfunktion zur Basis a:

Aus dem Rechengesetz der Multiplikation von Potenzen gleicher Basis folgt die sogenannte Funktionalgleichung:

2. Exponentialfunktionen sind für die Beschreibung von Wachstums- und Zerfallsvorgängen bedeutsam. Als Beispiel sei der Zerfall eines radioaktiven Elements betrachtet. Bei radioaktivem Zerfall nimmt die Anzahl N(t) der Atome des aktiven Elements mit der Zeit t ab, da sie sich in Atome eines anderen Elementes umwandeln. Beträgt zur Zeit t = 0 die Anzahl der aktiven Atome N₀ = N(0), so ist die Anzahl der Atome in Abhängigkeit von der Zeit durch eine Funktion der Art

zu beschreiben.

Physikalische Untersuchungen haben ergeben, dass jedes radioaktive Element eine Halbwertszeit t_H besitzt, nach der sich die Anzahl der aktiven Atome halbiert hat. Beispiel: Sei  und ; dann halbiert sich alle 5 min der Bestand an aktiven Atomen:
 

t / min	N(t)
0
5
10
15
20
25

Ein solcher Verlauf lässt sich mit einer Exponentialfunktion mit 0 < a < 1 wiedergeben:

Die Basis a kann mithilfe der Halbwertszeit ermittelt werden:

Die Zerfallsfunktion lautet also

Die Ableitung der Zerfallsfunktion ist die Zerfallsgeschwindigkeit. Sie soll hier durch den Differenzenquotienten, also die mittlere Änderungsrate angenähert werden:

Da der Bestand N(t) sich beim Zerfall verringert, ist die Zerfallsgeschwindigkeit negativ.

Als Aktivität A(t) bezeichnet man die Anzahl von Zerfällen pro Zeiteinheit:

Die Werte lassen vermuten, dass sich Zerfallsgeschwindigkeit und Aktivität mit der gleichen Halbwertszeit t_H verändern wie der Bestand N(t) der aktiven Atome. Das würde bedeuten:

Der Betrag der Zerfallsgeschwindigkeit (und damit die Aktivität) wäre damit proportional zum momentanen Bestand an aktiven Atomen.

3. Wenn die Aktivität in Abhängigkeit von der Zeit bekannt ist und weiter noch die Anzahl N₀ vorliegt, kann aus diesen Daten der Bestand an aktiven Atomen rekonstruiert werden. Beispiel: Durch Messungen sei die Aktivität zu jeder Stunde bestimmt, d.h. A(t) liegt in Form einer Tabelle vor:
 

Der Anfangsbestand sei .

Die Aktivität wird durch den Differenzenquotienten angenähert:

Daraus ergibt sich

Beginnend bei t = 0 kann nun gerechnet werden:

Der Term , der bei diesen Rechnungen immer wieder auftritt, lässt sich geometrisch deuten als die Fläche eines Rechtecks im Aktivitätsdiagramm:

Anders gesagt: Der Bestand N(t) ergibt sich durch Integration der Aktivität:

Um die Genauigkeit zu verbessern, empfiehlt sich im vorliegenden Fall nicht Rechteckstreifen zu benutzen, sondern das Trapezverfahren zu verwenden.

Fragen und Übungen

1. Was ist der Unterschied zwischen einer Potenzfunktion und einer Exponentialfunktion?

2. Wie ist die „Exponentialfunktion zur Basis a“ definiert? Geben Sie die Definitions- und die Wertemenge an.

3. Wie lautet die Funktionalgleichung der Exponentialfunktion zur Basis a?

4. Welche Probleme entstehen, wenn in dem Term  beliebige reelle Werte für x eingesetzt werden?

5. Vereinfachen Sie: 

6. Welche Exponentialfunktion hat an der Stelle x = 2 den Funktionswert 5?

7. Legen Sie eine Wertetabelle an:
 

-3
-2
-1
0
1
2
3

Was fällt auf?
Welcher Zusammenhang besteht zwischen den Graphen von ?
Können Sie eine Begründung für Ihre Beobachtungen angeben?

8. Bestimmte Wachstumsprozesse können mit Exponentialfunktionen  beschrieben werden. Entsprechend zum Begriff der Halbwertszeit bei einem Zerfallsvorgang gibt es hier eine Verdoppelungszeit t_D, das ist das Teitintervall, in dem sich ein momentaner Bestand verdoppelt. Zeigen Sie, dass bei Kenntnis der Verdoppelungszeit sich die Basis a ermitteln lässt und dass gilt .

9. Bilden Sie für das exponentielle Wachstum  die mittlere Wachstumsgeschwindigkeit . Leiten Sie daraus die Vermutung ab, dass die Wachstumsgeschwin- digkeit proportional zum momentanen Bestand sein könnte: .

10. Zeigen Sie, dass beim exponentiellen Wachstum gilt: .