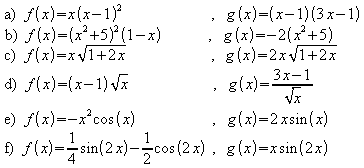3. Kettenregel

Die Funktion f mit  ist keine „einfache“ Wurzel-Funktion. Der Radikand ist ein quadratischer Funktionsterm:

Die Wurzel-Funktion

wird auf die Funktionswerte von v angewendet:

Dies nennt man eine Verkettung der beiden Funktionen u und v. Die Funktion u heißt äußere Funktion und die Funktion v wird innere Funktion genannt. Ene gebräuchliche Schreibweise ist auch , gelesen: „u verkettet mit v“. Die Definitionsmenge der Verkettung zweier Funktionen u und v ist .

Weitere Beispiele für Verkettungen von Funktionen:
 

Funktion	innere Funktion	äußere Funktion

Die Ableitung der Verkettung zweier Funktionen erfolgt wieder durch Rückgriff auf die Definition der Ableitung.

v(x) wird mit z abgekürzt und v(x+h) mit z + k:

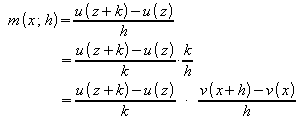
Wenn h gegen Null geht, dann geht auch k = v(x+h) - v(x) gegen Null. Damit ergibt sich:

Die Kettenregel lautet also:
 

Seien u an der Stelle v(x) und v an der Stelle x differenzierbare Funktionen. Dann ist die Verkettung f (x) = u(v(x)) an der Stelle x differenzierbar, und es gilt:

Merkregel: Die Ableitung einer Verkettung von Funktionen ist „äußere Ableitung mal innere Ableitung“.

Bemerkung: Bei obiger Herleitung der Kettenregel wurde vorausgesetzt, dass in einer kleinen Umgebung von x jeweils gilt . Es kann aber gezeigt werden, dass die Kettenregel für alle differenzierbaren Funktionen u und v gilt.

Anwendung auf die obigen Beispiele:
 

Funktion	Ableitung

Ein Anwendungsproblem:

Zwei Ortschaften A und B sollen eine Hochspannungsleitung mit elektrischer Energie versorgt werden. Die Entfernungen der Orte von der Leitung und voneinander sind der Zeichnung zu entnehmen. Wenn nur ein Transformator T benutzt wird, um die Hochspannung auf die benötigte Mittelspannung herabzusetzen, müssen zwei geradlinige Leitungen der Längen L_A bzw. L_B von T zu A bzw. zu B gelegt werden.

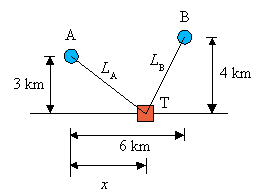
Wo muss der Transformator aufgestellt werden, wenn die Leitungslänge L = L_A + L_B möglichst klein sein soll?

Die Position des Transformators wird wie in der Zeichnung mit x bezeichnet. Dann ergibt sich für die gesamte Leitungslänge

Die notwendige Bedingung für lokale Extrema ist .

Mit der Kettenregel ergibt sich

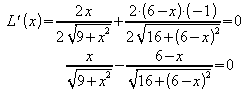Auflösen nach x:

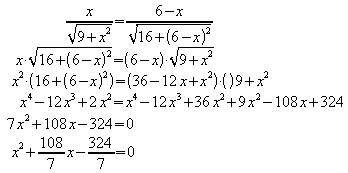
Lösungen dieser Gleichung sind

x₂ ist keine Lösung des praktischen Problems.

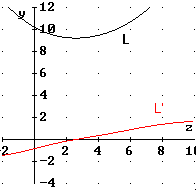
Um zu prüfen, ob eine Minimalstelle vorliegt, wird zweckmäßig das Vorzeichenwechselkriterium verwendet:

L' hat einen Vorzeichenwechsel von – nach +, also ist  eine lokale Minimalstelle.

Übungen

Leiten Sie jeweils mit der Kettenregel ab.

1.

2.

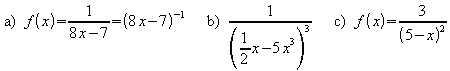
3.

4. Leiten Sie mit Produkt- und Kettenregel ab.

5. Leiten Sie mit Quotienten- und Kettenregel ab.

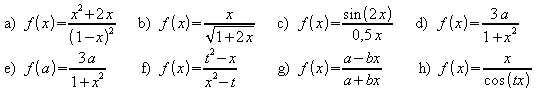
6. Ist f eine Stammfunktion von g?