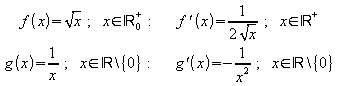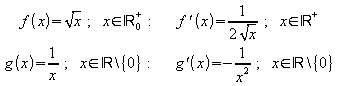.
.
Aus diesen Funktionen und den ganzrationalen Funktionen können weitere Funktionen gebildet werden, z.B.:
Um solche Funktionen abzuleiten, werden weitere Regeln benötigt.
zu berechnen. Eine erste Vermutung könnte sein, dass jeder Faktor
für sich abzuleiten ist:
Der Graph von f lässt schon einige Aussagen über f ' machen:
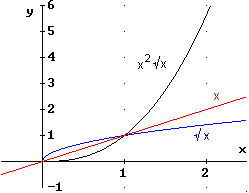
Es scheint, dass bei x = 0 eine waagerechte
Tangente vorliegt, also: 
.
Der Graph von f steigt stets an, also:
.
Außerdem wird der Graph mit wachsendem x immer steiler, d.h.
die Werte von f ' (x) werden immer größer.
Der Graph von 
gibt dieses Verhalten nicht wieder. Die obige Vermutung über die Ableitung
von f trifft daher nicht zu.
Die Ableitung einer Funktion war definiert als Grenzwert des Differenzenquotienten:
.
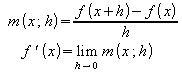Angewendet auf die vorliegende Funktion:
Der Zähler kann geometrisch als Differenz zweier Rechteckflächen gedeutet werden.
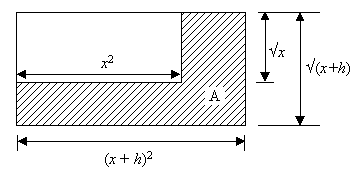
Die schraffierte Fläche kann auch wie folgt zusammengesetzt werden:
.
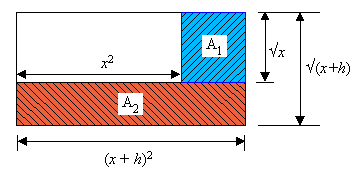
Damit wird der Differenzenquotient
,
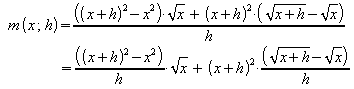und im Grenzwert ergibt sich
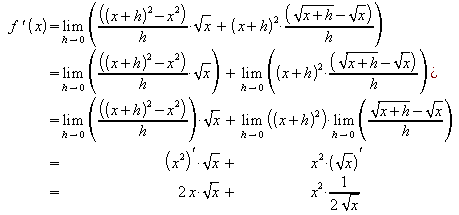
Nun soll der allgemeine Fall betrachtet werden,
dass die Funktion f das Produkt zweier Funktionen u und v
ist: 
.
Der Differenzenquotient lautet
.
Der Zähler kann wie in obigem Beispiel geometrisch als Differenz zweier Rechteckflächen gedeutet werden.
Die schraffierte Fläche kann wieder zusammengesetzt werden:
.
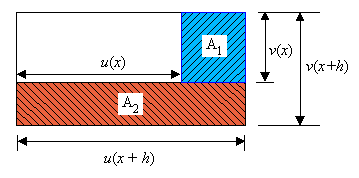
Für den Differenzenquotienten lässt sich also schreiben
,
und im Grenzwert ergibt sich
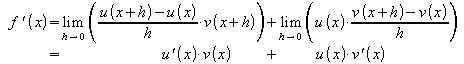
Damit ist die Produktregel gefunden:
Sei und
u und v seien an der Stelle x differenzierbar. Dann
ist auch uv an der Stelle x differenzierbar, und es gilt
|
Beispiele:
1) 
:
Hier ist 
.
Anwenden der Produktregel ergibt
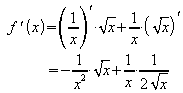
2) 
:
3) 
:
Hier ist natürlich die Summenregel zu berücksichtigen, und jeder Summand stellt ein Produkt dar, das nach der Produktregel abzuleiten ist:
Übungen
Leiten Sie jeweils mit der Produktregel ab.
Zur Erinnerung: Die Ableitungen der Sinus- und der Kosinusfunktion sind
.
1.
2.
3.
.