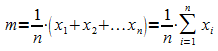
Der (arithmetische) Mittelwert von n gegebenen Zahlen x1, x2, ..., xn ist bekanntlich
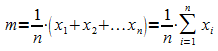
Diese Begriffsbildung lässt sich auf die Funktionswert f(x) einer auf einem Intervall [a; b] stetigen Funktion f übertragen:
Das Intervall [a; b] wird in n Teilintervalle der Länge 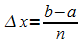 geteilt.
geteilt.
In jedem Teilintervall wird eine Stelle xi und der zugehörige Funktionswert f (xi) gewählt.
Damit wird der (arithmetische) Mittelwert gebildet: 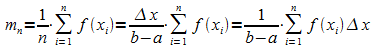 .
.
Für 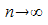 gilt
gilt 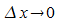 und
und 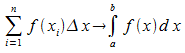 .
.
Definition: Für eine auf einem Intervall [a; b] stetige Funktion f heißt
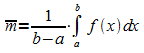
der Mittelwert der Funktionswerte von f auf [a; b].
Dieser Mittelwert der Funktionswerte ist selbst auch ein Funktionswert von f, wie der folgende Satz verdeutlicht:
Mittelwertsatz
der Integralrechnung: Ist f eine auf dem Intervall [a;
b] stetige Funktion, dann gibt es ein 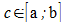 ,
so
dass gilt:
,
so
dass gilt:
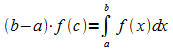
Zu beachten ist, dass c im allgemeinen nicht (a + b)/2 ist.
|
Wenn f im Intervall [a; b] nur positive
Werte |
|
Ergänzend sei angemerkt, dass es auch für die Differentialrechnung einen Mittelwertsatz gibt:
Mittelwertsatz der Differentialrechnung: Ist f eine im geschlossenen Intervall [a; b] stetige und im offenen Intervall ]a; b[ differenzierbare Funktion, dann gibt es (mindestens) eine Stelle c mit a < c < b, so dass gilt:
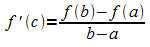
|
Geometrische Deutung: Der Graph von f nimmt in
(mindestens) einem Punkt die "mittlere Steigung" an, die durch die
Sekantensteigung |
|
Beispiel:
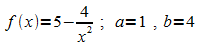
|
Integral: Mittelwert der Funktionswerte: Stelle c, für die gilt
|
|
|
Ableitung:
Sekantensteigung:
Stelle c, für die gilt
|
|
Gegeben sei eine auf dem Intervall [a;b] stetige Funktion. Der Graph von f schließt mit der x-Achse und den Geraden mit den Gleichungen x = a und x = b eine Fläche ein. Rotiert diese Fläche um die x-Achse, entsteht ein Rotationskörper.
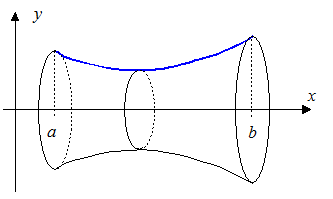
Das
Volumen eines solchen Rotationskörpers lässt sich ähnlich
berechnen wie die Fläche unter dem Graphen einer Funktion. Dazu
wird das Intervall [a; b] wieder in n gleiche
Teile der Breite 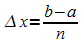 eingeteilt. Zu jedem Teilintervall gibt es einen Zylinder, der den
Körper von innen, und einen Zylinder, der den Körper von
außen berührt. Weiter wird in jedem Teilintervall ein xi
gewählt, so dass f (xi) zwischen den
Radien des inneren und des äußeren Zylinders liegt.
eingeteilt. Zu jedem Teilintervall gibt es einen Zylinder, der den
Körper von innen, und einen Zylinder, der den Körper von
außen berührt. Weiter wird in jedem Teilintervall ein xi
gewählt, so dass f (xi) zwischen den
Radien des inneren und des äußeren Zylinders liegt.
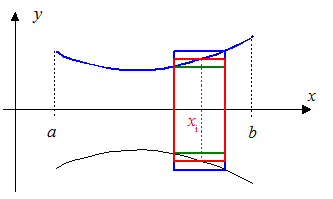
Damit ergibt sich für das Volumen des Rotationskörpers die Zerlegungssumme
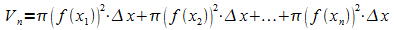 .
.
Im
Grenzwert 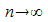 strebt die Summe Vn gegen das Integral
strebt die Summe Vn gegen das Integral 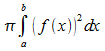 .
.
|
Satz: Ist die Funktion f auf dem Intervall [a; b] stetig, so entsteht bei der Rotation der Fläche zwischen dem Graphen von f und der x-Achse über [a; b] ein Körper mit dem Volumen
|
Übungen
1. Der
Graph der Funktion f mit 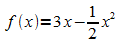 schließt mit der x-Achse eine Fläche ein. Berechnen Sie das
Volumen des Rotationskörpers, der bei Drehung
dieser Fläche um die x- Achse entsteht.
schließt mit der x-Achse eine Fläche ein. Berechnen Sie das
Volumen des Rotationskörpers, der bei Drehung
dieser Fläche um die x- Achse entsteht.
2. a) Wenn
ein Halbkreis mit Radius r und Mittelpunkt M(0|0) um die
x-Achse rotiert, entsteht eine Kugel mit Radius r.
Leiten Sie daraus die Volumenformel für die Kugel 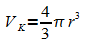 her.
her.
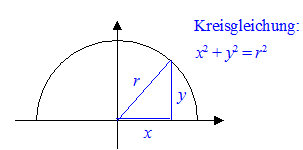
b) Bestimmen Sie das Volumen eines Kugelabschnitts mit der Höhe h und Kugelradius r.
3. Für
das Volumen eines Kegels mit Grundkreisradius r und Höhe
h gilt 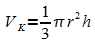 .
Leiten
Sie diese Formel her, indem Sie den Graphen einer geeigneten
Funktion um die x-Achse rotieren lassen.
.
Leiten
Sie diese Formel her, indem Sie den Graphen einer geeigneten
Funktion um die x-Achse rotieren lassen.
4. a) Begründen
Sie: Der Graph von 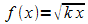 ist ein Ast einer um 90° gedrehten Parabel.
ist ein Ast einer um 90° gedrehten Parabel.
Rotiert der
Graph um die x-Achse, entsteht daher ein Rotationsparaboloid.
b) Der
lichte Raum eines Kessels hat die Form eines Rotationsparaboloides.
Der größte Durchmesser ist d, die Höhe h.
Zeigen Sie: Das Volumen des Rotationsparaboloides ist 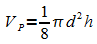 .
.
c) Die Maße des Kessels in b) seien d = 80 cm und h 60 cm. Berechnen Sie das Volumen in dm3. Bei welcher Höhe ist der Kessel halb gefüllt?
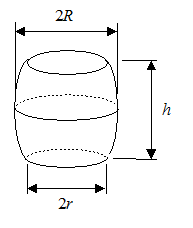
5. Ein
Fass hat die Höhe h = 1,2 m und die Radien r =
0,80 m und R = 1,0 m. Bestimmen Sie sein Volumen. Wählen
Sie dazu ein geeignetes Koordinatensystem und bestimmen Sie eine
quadratische Funktion f, über deren Graph Sie das Fass
als Rotationskörper erhalten.
.
Es soll die Länge eines Graphen einer Funktion f über einem Intervall [a; b] ermittelt werden. Vorausgesetzt wird: f ist im Intervall [a; b] differenzierbar und die Ableitung f ' ist stetig.
Zunächst wird eine Teilung des Intervalls [a; b]
in n gleich lange Teilintervalle
[xi ; xi + 1]
vorgenommen.
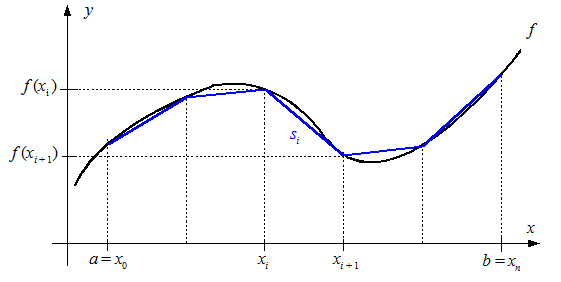
Über jedem Teilintervall wird die zum Graphen von f gehörige Sehne si gezeichnet. Auf diese Weise wird dem Graphen von f zwischen a und b ein Sehnenzug einbeschrieben.
Für die Länge si der Sehne über dem Teilintervall [xi ; xi + 1] gilt
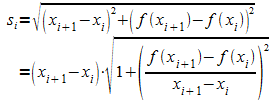
Nach dem Mittelwertsatz der Differentialrechnung gibt es ein 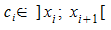 ,
für das gilt
,
für das gilt 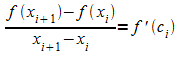 .
Für
die Länge der Sehne über dem Intervall [xi ; xi
+ 1] gilt daher:
.
Für
die Länge der Sehne über dem Intervall [xi ; xi
+ 1] gilt daher:
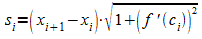
Die Länge des Sehnenzuges ergibt sich damit zu
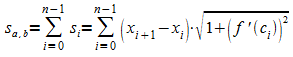
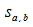 ist
für
jedes
ist
für
jedes 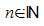 eine Riemann-Summe der Funktion
eine Riemann-Summe der Funktion 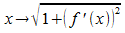 .
Da
f nach Voraussetzung auf [a ; b]
differenzierbar und ihre Ableitung dort stetig ist, ist auch die
Funktion
.
Da
f nach Voraussetzung auf [a ; b]
differenzierbar und ihre Ableitung dort stetig ist, ist auch die
Funktion 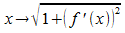 stetig. Daher existiert der Grenzwert der Summen
stetig. Daher existiert der Grenzwert der Summen 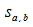 und ist gleich dem Integral.
und ist gleich dem Integral.
Damit kann die Bogenlänge des Graphen einer Funktion definiert werden:
Ist f eine auf dem Intervall [a ; b] differenzierbare Funktion, deren Ableitung dort stetig ist, so besitzt der Graph von f zwischen x = a und x = b die Bogenlänge
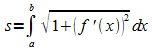
Anzumerken
ist, dass dieses Integral nur in einfachen Fällen mit einer
Stammfunktion gelöst werden kann. Eine numerische Lösung
ist unter den genannten Voraussetzungen jedoch stets möglich.