7. Numerische Integration

Wenn bei der Berechnung eines Integrals  keine Stammfunktion bestimmt werden kann oder wenn der Integrand nur in Form einer Wertetabelle vorliegt, muss man sich mit einer näherungsweisen Berechnung begnügen. Da hier nur der Zahlenwert (der numerische Wert) eines bestimmten Integrals ermittelt wird, spricht man von numerischer Integration.

7.1 Annäherung durch Geradenstücke

7.1.1 Rechteckverfahren

Zu bestimmen sei . Dazu wird das Intervall [a;b] in n gleich große Teile geteilt. Zu den Teilintervallmitten x_i werden die Funktionswerte f (x_i) ermittelt und damit folgende Summe gebildet:

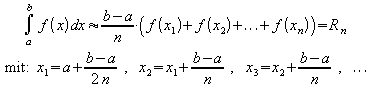
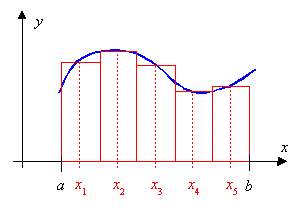
Beispiel: Zu bestimmen ist ein Näherungswert für .

Es wird n = 5 gewählt. Die Berechnung mit einer Tabellenkalkulation ergibt:

7.1.2 Trapezverfahren

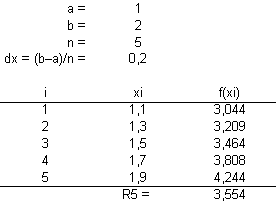
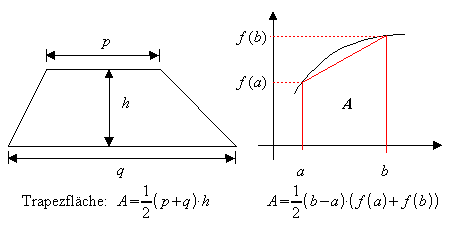
Das Intervall [a;b] wird in n gleich breite Teilintervalle der Breite (b – a)/n zerlegt und in jedem Teilintervall die einfache Trapezformel angewendet.

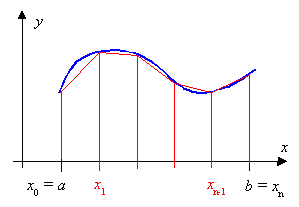
Insgesamt ergibt sich so:

Außer für x₀ = a und x_n = b kommen die Funktionswerte an den inneren Stellen x_i alle doppelt vor, so dass einfacher geschrieben werden kann:

Beispiel: wird mit dem Trapezverfahren für n = 5 näherungsweise berechnet.

7.2 Annäherung durch Parabeln

Nach Kepler ersetzt man den Graphen von f zwischen a und b durch eine Parabel, die durch  verläuft.

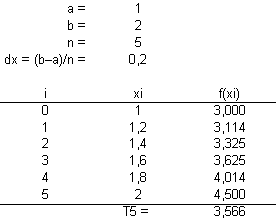
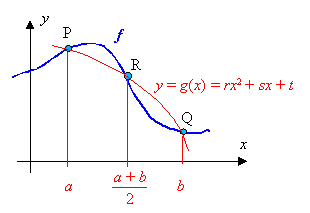
Wie hier nicht gezeigt werden soll gilt dann die Kepler'sche Fassregel:

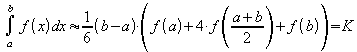
Beispiel: wird mit der Kepler'schen Fassregel näherungsweise berechnet.

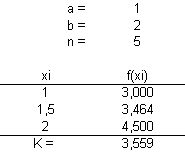
Mit einem Computer-Algebra-System ergibt sich auf 10 Stellen nach dem Komma:

Vergleich mit den drei verwendeten Näherungsverfahren:

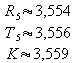
Zur Beurteilung von solchen numerischen Näherungswerten ist Kenntnis über den maximalen Fehler des verwendeten Näherungsverfahrens nötig. Solche Untersuchungen werden in der numerischen Mathematik angestellt – hier muss darauf verzichtet werden.