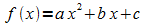.
Wegen der vorgegebenen Nullstellen ist
Eine ganz-rationale Funktion vom Grad 2 hat die Nullstellen x01 = 0 und x02 = 4. Sind damit die Extremstelle und der Extremwert der Funktion bereits festgelegt?
Die Funktion ist von der Form .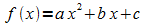
Wegen der vorgegebenen Nullstellen ist
f ist also nicht eindeutig festgelegt: die Funktionsgleichung
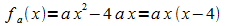
enthält noch den Parameter a. Für die Extremstelle von fa gilt:
.
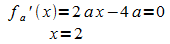Diese ist für alle Funktionen fa gleich. Die lokalen Extrema
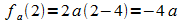
hängen jedoch von a ab.
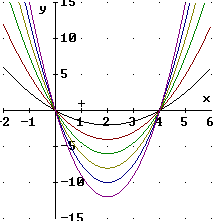
Def.: Enthält ein Funktionsterm außer der Funktionsvariablen x noch eine weitere Variable a (Formvariable; Parameter), so gehört zu jedem möglichen Wert von a eine Funktion fa: x --> fa(x). Die Menge dieser Funktionen nennt man eine Funktionenschar, ihre Graphen Ga eine Kurvenschar.
Beispiel 1:
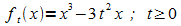
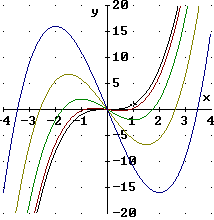
(Diese Funktionenschar können Sie auch mit einem interaktiven
Java-Applet darstellen: [ Beispiel
1 ].)
Symmetrie:
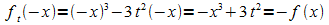
Der Graph Gt ist also punktsymmetrisch zum Ursprung.
Nullstellen von ft :
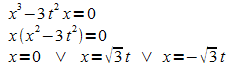
Ableitungen:
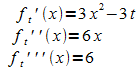
Hoch- und Tiefpunkte des Graphen Gt:
|
notwendige Bedingung: |
f t' (x) = 0 |
|
|
|
|
hinreichende Bedingung: |
|
|
x = –t: |
xe1 = –t ist also lokale Maximalstelle; lokales Maximum: Hochpunkt:
|
|
x = t: |
Wegen der Punktsymmetrie ist xe2 = t lokale Minimalstelle; lokales Minimum: Tiefpunkt: |
Weitere Untersuchungen
a) Für welchen Wert von t geht Gt durch A(3|0)?
Die Schnittstelle mit der positiven x-Achse ist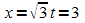 
,
daraus folgt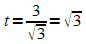 
.
b) Für welchen Wert von t ist die Gerade mit der Gleichung y = –x Tangente im Ursprung?
Die Tangentensteigung ist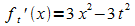 
,
also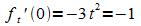 
.
Daraus folgt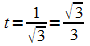 
.
c) Für welchen Wert von t ist die Tangente im Schnittpunkt mit der positiven x-Achse parallel zur Geraden mit der Gleichung y = x ?
;
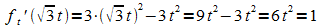daraus folgt 
.
d) Auf welcher Kurve liegen die Hochpunkte der Kurvenschar?
Die x-Koordinaten der Hochpunkte sind x = –t, also ist t = –x. Dies wird in die y-Koordinate der Hochpunkte eingesetzt:
.
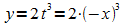Die gesuchte Kurve hat also die Gleichung
.
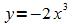Beispiel 2:
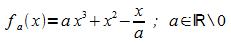
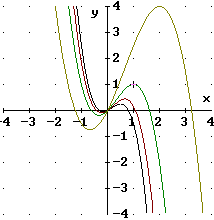
a) Zeigen Sie, dass jeder Graph Ga genau 3 Schnittpunkte mit der x-Achse hat.
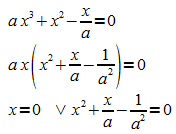
Lösungen der quadratischen Gleichung sind:
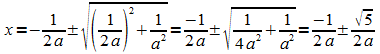
b) Zeigen Sie, dass jeder Graph Ga genau einen Hochpunkt und einen Tiefpunkt besitzt und bestimmen Sie diese Punkte.
Ableitungen:
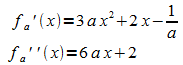
Untersuchung auf lokale Extrema:
|
notwendige Bedingung: |
f a' (x) = 0 |
|
|
|
|
hinreichende Bedingung: |
|
|
|
xe1 = –1/a ist also lokale Maximalstelle; lokales Maximum:
Hochpunkt:
|
|
|
xe2 = 1/3a ist also lokale Minimalstelle; lokales Minimum:
Tiefpunkt: |
c) Auf welcher Kurve liegen die Extrempunkte?
Hochpunkte: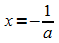 
,
also 
.
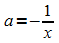Einsetzen in die y-Koordinate der Hochpunkte:
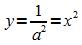
Tiefpunkte: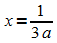 
,
also 
.
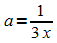Einsetzen in die y-Koordinate der Tiefpunkte:
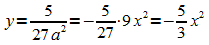
Beispiel 3:
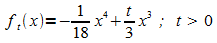
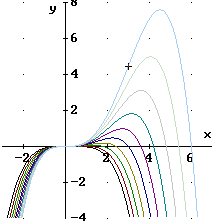
a) Funktionsuntersuchung:
Symmetrie: nicht erkennbar
Nullstellen: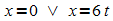 
Hochpunkte: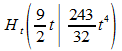 
Die Hochpunkte liegen auf der Kurve mit der Gleichung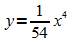 
.
Wendepunkte: W1(0|0) (Sattelpunkt)
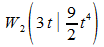
b) Haben die Graphen Gt außer (0|0) weiter gemeinsame Punkte?
Für gemeinsame Punkte gilt:
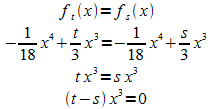
Dies ist für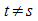
nur
für x = 0 erfüllt; es gibt also keine weiteren
gemeinsamen Punkte.
Übungen:
1. Durch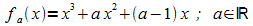 
ist eine Funktionenschar gegeben. Die zugehörigen Graphen seien
Ga.
a) Zeigen Sie, dass alle Graphen Ga zwei Punkte gemeinsam haben.
b) An welcher Stelle x0 haben alle Graphen Ga die gleiche Steigung? Wie groß ist diese?
2. Durch 
ist eine Funktionenschar gegeben. Die zugehörigen Graphen seien
Ga.
a) Bestimmen Sie die Schnittpunkte von Ga mit den
Koordinatenachsen, Hoch- Tief- und Wendepunkte. Zeichnen Sie G2
für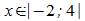 
.
b) Die Normale von Ga im von O(0|0) verschiedenen Wendepunkt W schneidet die x-Achse in P. Berechnen Sie den Flächeninhalt A des Dreiecks OPW. Für welches a beträgt A 13 Flächeneinheiten?
;
;
