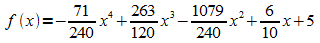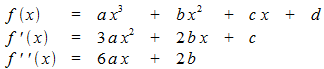
Beispiel 1:
Zu bestimmen ist eine ganz-rationale Funktion f vom Grad 3, deren Graph folgende Eigenschaften hat:
T(3 | f (3)) ist Tiefpunkt;
W(1 | 2/3) ist
Wendepunkt;
die Tangente im Wendepunkt hat die Steigung –2.
Die allgemeine Form einer ganz-rationalen Funktion vom Grad 3 ist
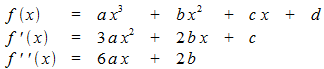
Die angegebenen Bedingungen führen zu einem Gleichungssystem für die zu bestimmenden Koeffizienten a, b, c, d.
T(3 | f(3)) ist Tiefpunkt: das heißt, an der Stelle x = 3 ist die Steigung 0, also:
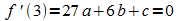
W(1 | 2/3) ist Wendepunkt: daraus ist abzulesen, dass an der Stelle x = 1 die zweite Ableitung 0 ist:
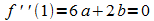 ,
,
und außerdem, dass an der Stelle x = 1 der Funktionswert 2/3 beträgt:
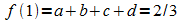 .
.
Im Wendepunkt ist die Steigung der Tangente –2: an der Wendestelle x = 1 hat die Ableitung den Wert –2:
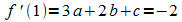 .
.
Gleichungssystem:
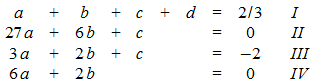
erste Umformung:
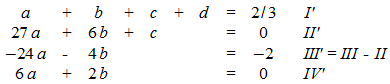
zweite Umformung:
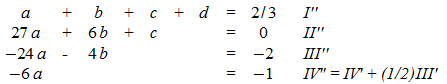
IV'' ergibt: 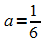
III'': 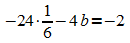 ,
also:
,
also: 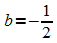
II'': 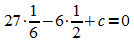 ,
also:
,
also: 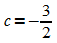
I'': 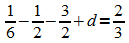 ,
also:
,
also: 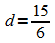
Die gesuchte Funktion (und ihre Ableitungen) lauten:
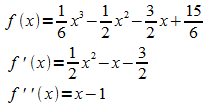
Probe:
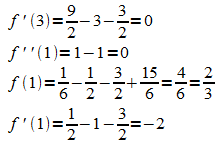
Beispiel 2:
Zu bestimmen ist eine ganz-rationale Funktion f vom Grad 3, deren Graph folgende Eigenschaften hat:
T(3 | –6) ist Tiefpunkt;
0 und –3 sind
Nullstellen.
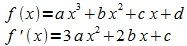
Die angegebenen Bedingungen führen auf die Gleichungen:
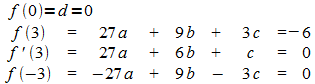
Lösung:
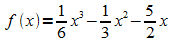
Beispiel 3:
Zu bestimmen ist eine ganz-rationale Funktion f vom Grad 3, deren Graph folgende Eigenschaften hat:
H(1| 1) ist Hochpunkt;
W(3 | f(3)) ist
Wendepunkt;
N(0 | 0) liegt auf dem Graphen.
Gleichungssystem:
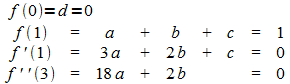
Lösung:
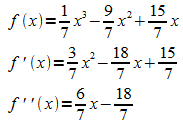
Beispiel 4:
Zu bestimmen ist eine ganz-rationale Funktion f vom Grad 3, deren Graph folgende Eigenschaften hat:
es liegt Symmetrie zum Ursprung (Nullpunkt) vor;
die
Steigung im Punkt P(1 | 1) des Graphen beträgt –1.
Die Symmetrie zum Ursprung bedeutet, dass f (–x) = –f (x) ist. Vergleicht man
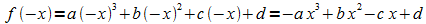
mit
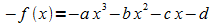 ,
,
so kann Gleichheit nur auftraten, wenn b = d = 0 ist.
Die weiteren Bedingungen führen zu folgenden Gleichungen:
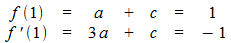
Lösung:
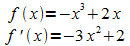
Beispiel 5:
Zu bestimmen ist eine ganz-rationale Funktion f vom Grad 4, deren Graph den Punkt H(2 | 4) als Hochpunkt und im Koordinatenursprung die Gerade mit der Gleichung y = x als Wendetangente hat.
Die allgemeine Form einer ganz-rationalen Funktion vom Grad 4 ist
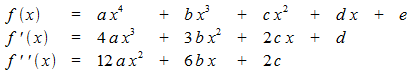
Aus den Bedingungen ergeben sich folgende Gleichungen:
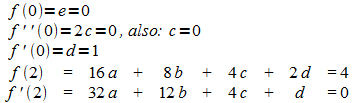
Lösung:
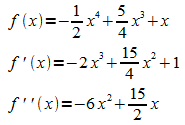
Übungen:
1. Der Graph einer ganz-rationalen Funktion f
vom Grad 4 ist symmetrisch zur y-Achse. Sie hat im Punkt P(2 | 0)
die Steigung 2 und den Wendepunkt W(-1 | f
(–1)).
Wie lautet die Funktion?
2. Der Graph einer ganz-rationalen Funktion vom Grad 3 geht durch den Ursprung des Koordinatensystems. Er hat in P(1 | 1) einen Hochpunkt und die Stelle x = 3 ist Wendestelle. Bestimmen Sie die Funktion.
3. Der Längsschnitt einer Rutschbahn soll durch eine
ganz-rationale Funktion vom Grad 4 beschrieben werden.
Die Bahn
soll in S(0 | 5) starten, dann durch P(1 | 3) verlaufen und in Q(4 |
0) enden. Die Steigung des Funktionsgraphen soll im Startpunkt S
den Wert 0,6 und im Punkt P den Wert –3 haben.
Lösungen:
1. 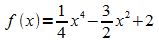
2. 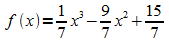 x
x
3.