MuPAD Light – eine kurze Vorstellung

1. Starten von MuPAD Light

Nach der erfolgreichen Installation von MuPAD Light ist eine Programmgruppe vorhanden, die in üblicher Weise über Start/Programme erhalten wird.

Mit Klick auf MuPAD Light wird das Programm gestartet.

Das Programm bietet zahlreiche Hilfen, die über das Menü Help aufgerufen werden können:

Browse Manual... – hier kann man das online-Handbuch durchsuchen;
Open Tutorial – eine sehr umfangreiche Anleitung (auch als Buch in Deutsch erhältlich);
Help Topics – eine kurze Einführung in die wichtigsten Funktionen.

2. Rechnen

Die Eingaben erfolgen direkt am Prompt (ein Punkt).

Befehle werden durch Semikolon abgeschlossen und mit ENTER ausgeführt. Das Ergebnis der Operation wird in blauer Schrift angezeigt. Wird eine Eingabe mit Doppelpunkt abgeschlossen, wird die Ausgabe des Ergebnisses unterdrückt. In einer Zeile können mehrere Befehle eingegeben werden, die durch Semikola zu trennen sind.

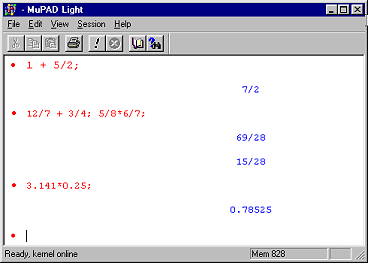
Die Operatoren für die Grundrechenarten sind

+ : Addition
– : Subtraktion
* : Multiplikation
/ : Division
^ : Potenzieren

Die Quadratwurzel erhält man mit sqrt(...).

MuPAD rechnet dabei „exakt“. Wenn dezimale Näherungswerte gewünscht sind, muss die Funktion float benutzt werden. Die angezeigte Anzahl von Dezimalziffern ist in der sog. „Umgebungsvariablen“ DIGITS festgelegt. Voreingestellt ist der Wert 10. Mit dem Befehl
DIGITS := ... kann jeder andere gewünschte Wert eingestellt werden.

float(sqrt(2));
                    1.414213562
DIGITS := 3;
                    3
float(sqrt(2));
                    1.41
DIGITS := 50:
float(sqrt(2));
                    1.4142135623730950488016887242096980785696718753769 Bei arithmetischen Operationen mit Zahlen rechnet MuPAD automatisch immer näherungsweise, sobald eine der beteiligten Zahlen in Gleitkommadarstellung gegeben ist.

(1 + (3/4*7))/(2/7 + 5/8)^2;
19600/2601

vergleiche dagegen:

(1.0 + (3/4*7))/(2/7 + 5/8)^2;
7.535563245

3. Algebra

MuPAD besitzt mehrere Funktionen zum symbolischen umformen von Termen, von denen hier 3 kurz vorgestellt werden sollen.

expand(...): Der eingegebene Ausdruck wird „expandiert“, wenn er eine symbolische Summe ist, die vereinfacht werden kann.

expand((x+y)^2);
                            2   2
                   2 x y + x + y
expand(sqrt(x+y));
                           1/2
                  (x + y)
expand(sin(x+y));
                    cos(x) sin(y) + cos(y) sin(x) Das Gegenstück dazu ist der Faktorisierer factor:

factor(x^2 + 2*x*y + y^2);
                            2
                    (x + y)
factor(x^3 + 3*x^2 + 3*x + 1);
                          3
                   (x + 1)

Ein universeller Vereinfacher ist die Funktion simplify(...), mit dem MuPAD eine möglichst einfache Darstellung eines Ausdrucks zu erreichen versucht.

f := 2^x * 3^x / (8^x * 9^x) : f = simplify(f);

                      x x
                     2 3          x
                   ------ = (1/12)
                     x x
                     8 9

4. Funktionen

Eine Möglichkeit, in MuPAD eigene Funktionen zu definieren, besteht in der Verwendung des Abbildungsoperators (Zuordnungsoperators) -> („minus“ „größer“).

f := x -> x^2:
f(x);
                     2
                    x
f(y);
                    2
                    y
f(x+y);
                          2
                    (x + y)
f(7/2);
                    49/4
f(3.5);
                    12.25
f(1+h);
                           2
                   (h + 1)

5. Funktionsgraphen

MuPAD verfügt über weitreichende graphische Möglichkeiten. Die einfachste Anwendung des Graphikmoduls ist das Darstellen von Funktionsgraphen. Dazu dient – neben anderen – die Funktion

plotfunc2d(f1, f2, ..., x = xmin..xmax, y = ymin..ymax)

f1, f2, ... : definierte Funktionen
x: die horizontale Koordinate
xmin..xmax: der horizontale Zeichenbereich
y: ein (Dummy-)Bezeichner für die vertikale Koordinate
ymin..ymax: der vertikale Zeichenbereich

f := x -> (x - 3)^2 - 2 :
g := x -> 1/2*x + 1 :

plotfunc2d(f(x), g(x), x = -2..8, y = -5 ..10);

Graphiken werden in eigenen Fenstern dargestellt:

f := x -> x^3 + 2*x^2 - 3*x - 2;
plotfunc2d(f(x), x = -5..5, y = -5..5);

6. Gleichungen

Zum Lösen von Gleichungen und Gleichungssystemen stellt MuPAD die Funktion solve(...) zur Verfügung.

f := x -> (x - 3)^2 - 2 :
g := x -> 1/2*x + 1 :
solve(f(x) = 0, x);
                      1/2        1/2
                    {2 + 3, 3 - 2 }
float(solve(f(x) = 0, x));
                    {1.585786438, 4.414213562}
solve(f(x) = g(x), x);
                     {            1/2    1/2      }
                    {          73     73         }
                    { 13/4 - -----, ----- + 13/4 }
                    {          4       4         }
float(solve(f(x) = g(x), x));
                    {1.113999064, 5.386000936}

7. Ableitungen

Die Ableitung einer Funktion kann auf verschiedene Weisen erhalten werden.

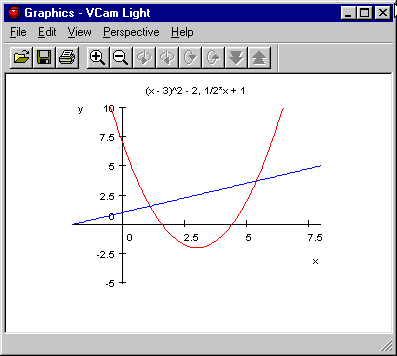
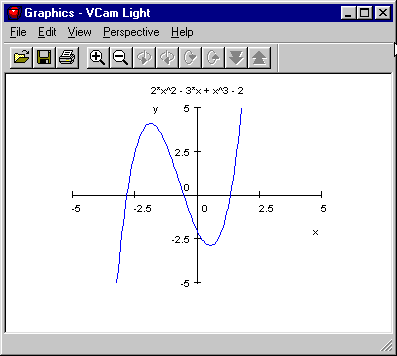
a) Verwendung der Funktion diff(...):

f := x -> x^3 + 2*x^2 - 3*x - 2;
diff(f(x),x);
2
4 x + 3 x - 3 Höhere Ableitungen:

diff(f(x),x,x);
6 x + 4
diff(f(x),x,x,x);
6 b) Verwendung des Differentialoperators ' :

f'(x);
                             2
                    4 x + 3 x - 3
f''(x);
                    6 x + 4
f'''(x);
                    6 Die Darstellung des Graphen einer Funktion und ihrer Ableitungen kann damit einfach durchgeführt werden:

plotfunc2d(f(x), f'(x), f''(x), x = -3..2, y = -5..5);

8. Integration

Mit der Funktion int(...) können Stammfunktionen ermittelt und bestimmte Integrale berechnet werden.

f := x -> x^3 + 2*x^2 - 3*x - 2:
int(f(x),x);
                        3     2          4
                    2 x    3 x          x
                    ---- - ---- - 2 x + --
                    3      2            4
int(f(x), x = -2..1);
                    3/4

9. Vektoren und Matrizen

Für Vektoren (und Matrizen) muss zuerst ein „Erzeuger“ definiert werden:

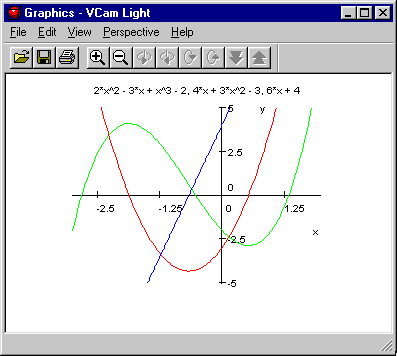
Erzeuger := Dom::Matrix();
Dom::Matrix()

Ein Spaltenvektor wird erzeugt, indem diesem Erzeuger eine Liste mit den Koordinaten des Vektors übergeben wird:

a := Erzeuger([1,2,3]);
    +- -+
    | 1 |
    |   |
    | 2 |
    |   |
    | 3 |
    +- -+
b := Erzeuger([4,3,5]);
    +- -+
    | 4 |
    |   |
    | 3 |
    |   |
    | 5 |
    +- -+

Addition von Vektoren:

a + b;
    +- -+
    | 5 |
    |   |
    | 5 |
    |   |
    | 8 |
    +- -+

Multiplikation eines Vektors mit einer rellen Zahl:

2*a;
    +- -+
    | 2 |
    |   |
    | 4 |
    |   |
    | 6 |
    +- -+

Auswahl der Koordinaten eines Vektors:

a[1];
    1
a[2];
    2
a[3];
    3

In der Programmbibliothek „linalg“ stellt MuPAD zahlreiche Funktionen zum Rechnen mit Vektoren und Matrizen zur Verfügung. Beispiel: das Skalarprodukt von Vektoren:

linalg::scalarProduct(a,b);
25

Damit kann der Betrag eines Vektors ermittelt werden:

abs_a := sqrt(linalg::scalarProduct(a,a));
1/2
14

Eine Matrix wird erzeugt, indem man dem Erzeuger eine geschachtelte Liste mit den Zeilen der Matrix übergibt:

A := Erzeuger([ [1,2,3], [4,2,3], [3,2,1] ]);
    +-       -+
    | 1, 2, 3 |
    |         |
    | 4, 2, 3 |
    |         |
    | 3, 2, 1 |
    +-       -+

Die Determinante kann mit einer Funktion der Bibliothek linalg berechnet werden:

detA := linalg::det(A);
12

Das Inverse einer Determinante ergibt sich aus

invA := A^-1;
    +-               -+
    | -1/3, 1/3, 0    |
    |                 |
    | 5/12, -2/3, 3/4 |
    |                 |
    | 1/6, 1/3, -1/2 |
    +-               -+

Multiplikation zweier Matrizen:

A*invA;
    +-       -+
    | 1, 0, 0 |
    |         |
    | 0, 1, 0 |
    |         |
    | 0, 0, 1 |
    +-       -+
B := Erzeuger([ [2,-1/3,-4], [3/5,2,-3], [-3/8,1,2] ]);
    +-           -+
    | 2, -1/3, -4 |
    |             |
    | 3/5, 2, -3 |
    |             |
    | -3/8, 1, 2 |
    +-           -+
A*B;
    +-                 -+
    | 83/40, 20/3, -4   |
    |                   |
    | 323/40, 17/3, -16 |
    |                   |
    | 273/40, 4, -16    |
    +-                 -+